Recursive Functions

A recursive function (of one or more variables) is such that its value at a given argument is expressed in terms of its values at smaller arguments or in terms of "simpler" functions. For example, the function f defined by

f(0) = 1, f(1) = 1, f(x+2) = f(x+l) + f(x),

which gives the Fibonacci sequence 1, 1, 2. 3, 5, 8, 13, ... is recursive. This Fibonacci function can be also defined directly:

x+1

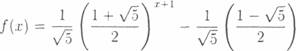
However not all recursive functions can be defined algebraically like this.   A more involved example is the function g of two variables defined by

g(x, 0) = x+1, g(0, y+1) = g(1, y). g(x+1, y+1) = g(g(x, y+1), y).