|
Plato on Knowledge |
|
|
|
|
|
Recommended Reading Crombie, I. M. (1963) An
Examination of Plato’s Doctrines (Vol. 2) London: Routledge &
Kegan Paul Text of Plato Cornford, F.M.
(1957) Plato’s Theory of Knowledge:
The Theaetetus and Sophist of Plato Indianapolis:
Bobbs-Merrill Cornford, F.M.
(1941) The Republic of Plato,
London:
OUP Plato (tr. W.K.C.
Guthrie, 1956) Protagoras and
Meno Harmondsworth:Penguin Plato |
|
|
Plato’s Later Theory of Knowledge |
|
|
In the Theaetetus Plato gives us his
final and most fully thought out discussion of knowledge. He begins by
proposing that knowledge is just what one perceives, but that idea is no
good for all the obvious reasons. His second attempt is to say that
knowledge is true belief, and, again, it is pretty easy to see that it
isn’t sufficient: it’s far too easy to come to have beliefs that are true
in inappropriate ways. The example he gives to make this case is that an
Athenian jury can be persuaded to believe something true is true, and yet
they are convinced “about things which only someone who sees them can
know”201b8: that is, they don’t have the right connection to
the things to be really knowledgeable about them. Finally he
proposes that knowledge is true belief with an account (meta logou
alêthê doxan). We would naturally suppose that what he has in mind
here is something similar to the standard modern view with his ‘account’
being the justification for the belief in the true thing. But it’s not at
all clear that this is what he means. In fact he gives us several versions
of the so-called ‘account.’ The first version he considers is the claim
(which he supposedly remembers being made in a passage known as
‘Socrates’s Dream’) that an account of X is an analysis of how X is
composed of simpler parts. An odd consequence of this is that if X is not composed of parts then there
can’t be such an account and we can’t know X – presumably they are
perceived. This suggests that those who hold this theory aren’t talking
about the same sort of thing that we are when we’re talking about
knowledge. In any case Plato thinks that if we can’t know the parts of
something then we can’t know the whole thing that they compose, which may
well be true if we’re using ‘know’ in the propositional knowledge’
sense. Another
version he wonders about is one that claims that the account is a
catalogue of the component parts. If you can list the simple elements of X
then you know X. This works for both complex and simple Xs, so it’s better
than the previous proposal; but it doesn’t take account of the fact that
real knowledge requires knowing how those parts go together to
form the complex. If someone knows what letters are in the name
‘Theaetetus’, but doesn’t know what order they go in, or how the letters
create syllables (perhaps a recent immigrant from China with no knowledge
of alphabets would be in that position,) then that person doesn’t ‘know’
the name ‘Theaetetus’. Finally,
Plato considers the idea that to give an account of X is to identify the
characteristic features of X that distinguishes it from all other things,
or even from all other things of the same kind. So, for example, to know
something about the sun is to have a true belief about the sun and to be
able to say that it is the brightest object in the heavens. To us, this
still seems to miss the point. It isn’t the identification of the object
that is the important thing about knowledge; it is trying to establish
grounds for believing the true thing that one does believe about the
object. In any case, to say that to know X is to have a true belief about
X and also to know something
else about it doesn’t work very well as a definition of knowledge. You
really can’t have the word you’re trying to define in your
definition. Plato
pretty much ends his discussion of knowledge there, leaving us apparently
without any acceptable definition of knowledge. This, you’ll recall, is
typical of the way these dialogues go: we called the Socratic style of
philosophy aporetic because of
this tendency to come to no conclusion. Despite this apparent failure, it
is sometimes said that in his later years Plato really did think that
knowledge was true belief with an account, because this dialogue is quite
a late one, and because it seems that other characters in his late
dialogues regularly assume something like its final description of
knowledge as true belief with an account This seems unlikely, however. I
think it is just as likely that Plato was defending his earlier theory of
knowledge by showing that these other theories could not be defended. In
any case, it’s this earlier theory that we’re going to look at
now.
|
|
|
The Theory of Forms |
|
|
The Theaetetus talks about knowledge
in a way that is quite familiar to us, but by far the most influential
Platonic theory – one which he never explicitly renounced – is one that is
never even hinted at in that dialogue. This theory is the theory of the
so-called ‘Forms’ or ideas. In
this theory Plato proposed that there was a realm of non-physical things –
the Forms – that really exist, and are somehow connected to the things
that really exist in the physical world. So there is a Form of a table
that is connected to things which are tables, and a Form of a dog
connected to things which are dogs. And this also applies to things which
can be taken as abstractions from the physical world: thus we have the
Form of courage, and the Form of triangle, and so on. Plato thought that
he could show both that there had to be such things as the Forms and that to know something was to be in some
way acquainted with the Form of that thing. It’s a fairly complicated idea
and we’ll start with the justification for the existence of the Forms at
all. The Problem
of Universals The first
argument for the Forms runs as follows. All things that are unambiguously
called by the same general term (e.g. milk, dog, book, hamburger) must be
so called in virtue of something which is (i) common to all things
properly called by that general term, and (ii) peculiar to (or
distinctive of) all things properly called by that general term. Now the
common and peculiar characteristic(s) of dogs are not physical properties;
after all, we can tell that something is a dog just by looking at it, but
not all dogs look the same. Similarly we can tell that something is a book
just by looking at it, but not all books look alike. We can even instantly
recognise that a book that we have never seen before is a book, even though it
is not exactly like any book we have seen before, or possibly like any
other book in the world. How do we do it? Plato’s
answer is that we must recognise that it embodies some characteristic
which is not discernible by our senses, which is common to all such things
and peculiar to all such things. This embodied characteristic is not a physical characteristic, but a
characteristic which our mind apprehends, and which is reflected or
embodied imperfectly in all and only (say) books. The Problem
of Judgement A second
and more enlightening argument comes from the nature and possibility of
judgement. For Plato (and many others) all judging is comparing. If I judge that this
liquid is milk, then I am implicitly invoking some standard of ‘milkiness’
and judging that this liquid compares favourably with that standard.
Similarly, if I judge of some other liquid that it is not milk, I must be
invoking the same standard and be judging that this other liquid does not
compare favourably with it. Similarly if I judge that something is, or is
not, a book, a computer, an aeroplane, a dog, etc. This
standard of comparison could not be another thing of the same type. If it
were, then I would have to judge that it, too, was a thing of that type,
and that would involve me in comparing it with something else. And of that
thing, too, I would have to judge that it, too …. And so on ad infinitum. We are away on what
philosophers and logicians call an infinite regress. In order to make
the first judgement I must make a second judgement, to make the second I
must make a third, to make the third, and so on forever. There can be no
end to this series, therefore I can never complete it; accordingly I can
never even make the first judgement. So, what is
the alternative? Presumably we must be comparing the liquid before us with
something that is not a liquid. Is it perhaps my mental image or mental
concept of milk? But why should the fact that something compares
favourably with my mental image or concept of milk make it milk?
Presumably it is because my mental image or concept of milk constitutes an
accurate likeness to or representation of milk. And to determine this I
would have to compare my mental image of milk or mental concept of milk
with something else. But with what? With real milk? But then I would have
to judge that what I was comparing my mental image (concept) of milk with
was real milk. So what do I compare that with? This is where we came
in. So the
standard of comparison appears to be neither physical (another example of
milk) nor mental (my mental image or concept of milk.) So what is left?
Plato’s answer is that the standard is neither physical nor mental but metaphysical (which means it is
something ‘beyond the physical.’) For the moment we can interpret this
expression negatively by saying that it is something that is real but
neither a physical thing nor a mental thing. (God, as commonly understood,
is a metaphysical being in this sense: if God is real, He is, even so,
neither a physical thing nor a mental thing.) The ultimate standard or Form of anything (be it milk, a dog, a book, or a hamburger) is that in virtue of which (i) all things properly called by that general term (‘milk’, ‘dog’, ‘book’, ‘hamburger’, etc.) are properly so called, and (ii) only things properly called by that general term are properly so called.
|
|
|
Those who Know, Know
the Forms |
|
|
Both
arguments lead to the same conclusion. So how do the Forms relate to the
particular things which ‘fall under’ or ‘instantiate’ them? For Plato
there are two dimensions to this relationship: (i)
Transcendence: there is
far more to the Forms than the particular things which fall under them
(for short – their particulars.) (ii)
Immanence: the Forms
are present in their particulars, though not in a way which is manifested
to the senses. Forms do
not exist in either physical reality or the mind. So how do we know of
them? We are not aware of the Forms through the five senses by which we
are informed of the external environment. Nor are we aware of them from
the one sense (sometimes called, e.g. by Kant, apperception) by which we are
informed of the contents of our own mind. Rather it is by what is
sometimes called ‘the mind’s eye’ – referred to in one place by Plato as
‘the eye of the soul’ – that we become aware of the Forms. He also
describes it as an ‘intellectual awareness’ or as a ‘perception by the
understanding’. (These are difficult concepts – concepts which some
critics say are ultimately incoherent.) The Form of
the dog is that with which I compare this animal that is before me when I
judge that it is, or is not, a dog. This example, like the examples of
milk, book, and hamburger, is an example of a mundane thing and a ‘lower
Form’. Although Plato is a little ambivalent on this he seems to say (and
his theory may well require him to say) that these are examples of Forms
which can be apprehended by
‘ordinary people’ (i.e. people un-schooled in philosophy) – after all they
succeed in making such judgements so they must be making the relevant
comparisons. These are sometimes called the ‘lower Forms’. But when it
comes to the ‘higher Forms’ he believes that they are beyond the reach of
most people without an appropriate education, including most importantly a
philosophical education. These higher Forms include the mathematical
standards, ethical and aesthetic standards e.g. just, right, noble, worthy, beautiful,
sublime, fitting, and the highest Form of them all (accessible only by
a very few), the Form of the
Good. Knowledge
Comes from Within But let’s
look at how we might come to know the higher Forms – in mathematics, for
example. In one of his dialogues, called the Meno, a slave is taught how
to double a square. And before you go on, you might like to pause and
consider whether you could solve the puzzle: given a square of a certain
area, construct a square of exactly twice the area. Here is how
Socrates proceeds:
SOCRATES: Mark now the
farther development. I shall only ask him, and not teach him, and he shall
share the enquiry with me: and do you watch and see if you find me telling
or explaining anything to him, instead of eliciting his opinion. Tell me,
boy, is not this a square of four feet which I have drawn?
BOY: Yes.
SOCRATES: And now I
add another square equal to the former one? BOY: Yes.
SOCRATES: And a third,
which is equal to either of them? BOY: Yes.
SOCRATES: Suppose that
we fill up the vacant corner? BOY: Very good.
SOCRATES: Here, then,
there are four equal spaces? BOY: Yes.
SOCRATES: And how many
times larger is this space than this other? BOY: Four times.
SOCRATES: But it ought
to have been twice only, as you will remember. BOY: True.
SOCRATES: And does not
this line, reaching from corner to corner, bisect each of these spaces?
BOY: Yes.
SOCRATES: And are
there not here four equal lines which contain this space?
BOY: There are.
SOCRATES: Look and see
how much this space is. BOY: I do not
understand. SOCRATES: Has not each
interior line cut off half of the four spaces? BOY: Yes.
SOCRATES: And how many
spaces are there in this section? BOY: Four.
SOCRATES: And how many
in this? BOY: Two.
SOCRATES: And four is
how many times two? BOY: Twice.
SOCRATES: And this
space is of how many feet? BOY: Of eight feet.
SOCRATES: And from
what line do you get this figure? BOY: From this.
SOCRATES: That is,
from the line which extends from corner to corner of the figure of four
feet? BOY: Yes.
SOCRATES: And that is
the line which the learned call the diagonal. And if this is the proper
name, then you, Meno's slave, are prepared to affirm that the double space
is the square of the diagonal? BOY: Certainly,
Socrates. SOCRATES: What do you
say of him, Meno? Were not all these answers given out of his own head?
MENO: Yes, they were
all his own. Socrates
makes the point then that in a certain sense the boy must be said to have
known the answer to the original question already, because all Socrates
did was get him to agree to certain questions, which he knew the answers
to – and by this process brought to the front of the boy’s mind his
knowledge of geometry. Now, Socrates goes on to make a strange claim that
this shows that we must have become acquainted with the Forms associated
with such knowledge in some pre-physical existence – but that’s not the
point that I want to make here. What’s important here is to realize that
Plato believes that knowledge of the Forms can be drawn out of all of us
by the process of education; and the better our education, the better our
ability to recognize the Forms in the world. The
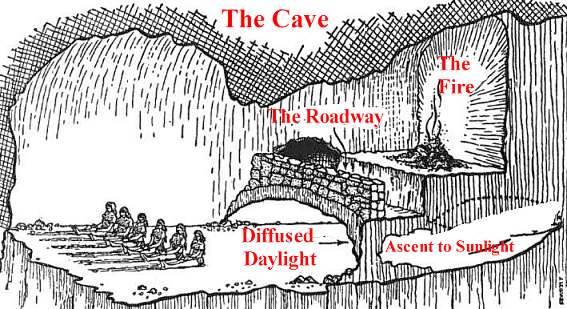
Allegory of the Cave In his Republic Plato gives a dramatic
and famous picture of how he sees the difference between the way that the
philosopher sees the world and the way that the untutored and uneducated
who cannot recognise the Forms see it. He invites us to imagine a cave
which descends gradually into the side of the hill. At the bottom of the
cave, facing the rear wall and unable to turn and see the mouth of the
cave, are a group of prisoners who are shackled to their positions on the
cave floor. All they can see are shadows on the rear wall of the cave in
front of them. They do not know how they came to be there – indeed all
knowledge of any past has been extinguished. They do not even know they
are prisoners. Some of them become good at predicting what shadows are
going to pass along the wall next as there are various patterns, some of
which repeat themselves. These unfortunate people would think that what
they were witnessing was reality. It would not occur to them that, far
from being reality, what they are seeing is actually a mere effect of
something far more substantial, of which they have no
conception.
We then imagine that somehow, a small
number of the prisoners manage to get free and after a painful struggle
succeed in turning their heads towards the mouth of the cave. What they
see is that, near the mouth of the cave there is a fire (something they
have never seen before) and passing between the fire and the prisoners are
various people carrying objects of various sorts. Unlike the shadows,
these entities are three-dimensional. Moreover, they see that there is a
correlation between the movement of entities in front of the fire and the
shadows that appear on the wall. Not only that but studying the movement
of these entities becomes a far better basis for predicting the successive
shadows than merely studying the recurring patterns among the shadows.
These people believe they have superior knowledge to the rest of
the prisoners. They have, they think, knowledge of the world as it is in itself (the
fire and the moving three dimensional entities are the true reality) in
terms of which they can explain the
world of mere appearance which the still bound prisoners naively and
falsely believe is the world as it really is (all that there is) – the
world of projected shadows. The prisoners who break free and see
the source of the shadows, and who learn how to predict the succession of
shadows more accurately, are analogous to natural scientists. Natural
scientists are constantly coming up with theories based on extrapolations
from observations that suggest that the world as it really is happens to
be very different from the world as it appears (e.g. the world appears to
contain colours but the scientific explanation of the appearance of colour
does not require the postulation of colours). But now we imagine a few brave prisoners who venture beyond the fire. After a struggle they vaguely see diffused daylight. They crawl and stumble further until eventually they get to the mouth of the cave itself – and then, filled with apprehension, they venture outside. At first they are simply dazzled by the brightness and cannot see anything. Then, as their eyes become accustomed to the light, they see colours they have never seen, objects and shapes they have never seen before, and a myriad of things for which they have no names. For Plato this is the intellectual world, and the journey, the last stage of which they have just completed, is the philosophical journey. These escapees correspond to the philosophers. They have ventured beyond mere appearances (the shadows on the cave wall) to seeing the things which the scientist would say are the genuinely real things and which explain the mere appearances. And now they have ventured beyond the world as understood by the scientist to ultimate reality – the world as it really is in itself. And this is the world of the true and ultimate nature of things. It is the world of the Forms.
|
|
|
What are the Objects of Knowledge? |
|
|
The way Plato talks about the degrees of knowledge in that Allegory of the Cave makes it pretty clear that Plato thinks that only the Forms are suitable objects of knowledge. Because of the changeability of perceptions they cannot be taken as the objects of knowledge – we can say nothing about them that is timelessly and indubitably true. Only those things which are eternally true and knowable purely intellectually are really to be considered as the objects of knowledge. In this respect, Plato is the founding member of one of the two great classes of epistemologists. The other great class, which considers the world and empirical fact to be the foundations of ‘real’ knowledge is represented by Aristotle. We shall consider his views in the next lecture.
|
|