Inductive Generalisation

In the last lecture I began to speak of a type of inductive reasoning or argument that is often taken to be – in argument textbooks anyway – the paradigmatic case of induction. The type of reasoning we’re going to be looking at is a type of Inductive Generalization, which are generalisations characterized by movement from the particular to the general. In fact an argument is an inductive generalisation if and only if a generalised conclusion about the character of some class as a whole is drawn from characteristics of a sample of the class – whether that class consists of light-bulbs or people or whatever. For that reason you’ll often see this sort of argument referred to as Sampling Arguments.  Such arguments are obviously generalisations, and they are inductive because not all members of the class in question need necessarily have the characteristics of the sample (as the conclusion suggests they do). It is, at best, highly likely.

I also mentioned the division of these arguments into the categories of strong and weak inductive and statistical generalisation. I’m not going to talk any more specifically about those types of induction because I want to concentrate attention on the remaining category, which is the class of generalisations which claim that some specific proportion of the members of the target class possess a certain property. Arguments like this are called Statistical Generalisations.

For example:

10% of people in this sample of the general population indicated they would vote for Bob.

------------------------------------------------------------------------------------------------------------

                10% of the general population would vote for Bob.

The reason that I want to talk about these in particular is because statistical arguments such as these seem to feature heavily in debates that occur in the process of public policy formation. You can see from the example I just gave that opinion polls are used to make statistical generalisations; and so too, of course, are surveys of health effects of drugs, and so are environmental samplings, and so on ad nauseam. So you can see how important they are. It’s not that all the other types of argument don’t occur but that these arguments with their aura of objectivity and quantified certainty are so very effective in debate. This being the case, and this being the sort of class where one might expect to find the policy drivers of the future, I take it that I will be performing a valuable public service in acquainting you with the important simple tools with which to cope with these arguments.

Evaluating Inductive Generalisation

So how should we approach an inductive generalisation? I’m going to go through a few things that are useful in trying to evaluate these arguments. Bear in mind as I do so that the examples I’ll be giving are of the statistical generalisation form but they can often be applied (with the appropriate changes) to all types of sampling argument.

1.                    Are the premises true?

The first thing to enquire after is whether the premisses are actually true. This question is always important to address. Did the sample really substantiate claims made about it in the premises? Does the premise, perhaps, merely report hearsay or popular opinion and not fact? There’s another problem too, It’s a fairly well-established fact that people are not always scrupulously honest in the responses that they give to political pollsters. There is a tendency for people who intend to vote for a conservative party to claim otherwise when questioned by pre-election pollsters, and they may even misreport their behaviour after they’ve just voted. This can lead to extreme embarrassment on the part of polling organizations when the election results come in. I seem to recall that polling data reported prior to the Nicaraguan elections indicated a near universal approval of the Sandinista government – which nevertheless lost by about 70%. Therefore be aware!

2.                    Is the sample lÿÿge eÿÿugh?

The justifiedness of sampling arguments depends upon an assumption that the sample is representative of the larger population – it is only if that is the case that we can feel happy in extending the discovered properties of the sample to the population. But a smallsample runs a very high risk of being unrepresentative just because the capacity for statistical anomaly is much greater in a small sample than in a large one. We’ll get beack to some technical talk about this in a moment, but for now it’s enough to consider that and example such as the results of coin tossing.

75% of observed coin tosses come up heads

-----------------------------------------------------

                        75% of all coin tosses will come up heads

That might seem reasonable until you are told that there have only been four coin tosses. It’s not that unusual that there be 3 heads in 4 tosses. If there had been 400 tosses then we’d be more impressed – but as I say, more on this later. Just bear in mind that a small sample may be unrepresentative and so suggest a general characteristic which does not apply.

a.        There is a characteristic error which is due to the tendency to generalize from restricted samples: it is called the Fallacy of Hasty Generalisation

Cognitive psychologists have noted our unreasonable tendency to see a small sample as truly representative (thus explaining our tendency to hastily generalise):

We submit that people view a sample randomly drawn from a population as highly representative, that is, similar to the population in all essential characteristics. Consequently, they expect any two samples drawn from a particular population to be more similar to one another and to the population than sampling theory predicts, at least for small samples.[1]

On the other hand, it is not generally the case that the substantial results of a survey will be affected by the size of the sample. What will change is the margin of error.

b.        There’s another fallacy closely related to this (or maybe it’s a variety of the same thing) that I’ve mentioned in passing before: that is the fallacy of anecdotal evidence.

There is a tendency for people to think that they can usefully respond to a statistical generalisation by saying that they know of a case in which the generalisation didn’t hold. For example:

                Bob: 80% of people who leave school before they’re 15 live in poverty.

Al: Nonsense. Why, both my parents left school before they graduated and they’re now running a million dollar business.

The point problem with this as a response, of course, is that the statements may both be true together and Al’s parents are some of the 20% of early school leavers that are claimed not to be living in poverty. We should also note that this is a much more common response (and apparently more plausible too) to merely weak inductive generalisations, but it’s just as misguided there.

3.                    Is the sample biased in some other way?

As I just said, it is the representativeness of the sample which makes it possible (by definition) for the result of testing the sample to be true of the population. If there is a bias in the sample then the sample will not be representative. The best way to try to make sure there are no biases is to select the sample randomly from the population. (If there is no systematicity in the selection there can be no systematic bias.) It is not easy to do this, however, and there is always the danger that a sample may be unrepresentative due to the method of sampling having been such as to select for particular characteristics. This leads to the Fallacy of Biased Sampling. I think you will find that it is far and away the most vulnerable spot at which to attack any result that you don’t like.

Bias can arise due to:

a.                   Insufficient variation in the sample

A large sample might still be unrepresentative of the whole population because it is badly

chosen. The following are some examples:

                        1.                        Using a phone book to get a large sample of the population.

Some of you will already have heard of the famous example of biased sampling that made the Literary Digest predict that Landon would defeat Roosevelt in the 1936 American Federal election. The problem was that the paper had selected its sample from the phone books of the various states. Unfortunately, that wasn’t a random sample, because at that time telephones were concentrated in the wealthier homes, and those homes were more likely to vote for Landon than the average American home.

[An example like this makes the point that a sample doesn’t have to be random in all possible dimensions in order to be a representative sample for a particular purpose (that can never be achieved at a reasonable cost), but it does have to be random in all the likely relevant dimensions. There’s a skill in deciding what those dimensions may be and knowing how to randomize on them.]

                        2.                        Using birth-order as a behavioural predictor

Suppose (as was actually done) you sample scientists to see what factors might pre-dispose someone to accept radical new theories. You discover that, of the people sampled, socio-economic factors do not vary with such a disposition yet birth-order does (i.e. the first born of the sample-set tend to be so disposed and the later born do not).               

Conclusion:          First-borns are more likely to accept radical new theories in general — a biological or "nature" factor, contra an account which might suggest the determining factor is socio-economic — "nurture".

Problem:                Cannot draw conclusion that birth-order is a more important  determinant of willingness to accept radical new theories per se since sample of scientists might not be representative of socio-economic variation.

3.     Basing inferences concerning the general behaviour of native pigeons, say, on their behaviour when you've observed them.

They always seem very nervous when I observe them and so I am tempted to conclude that they are quite nervous birds, but of course my initial data may simply reflect the fact that they're very nervous when being watched by a potential predator (namely, me)!

b.                   Eliciting a particular characteristic from the sample by Slanted Questions

Again, a very common trick. Compare the results that are reported in the following two polls on a topic of current interest, i.e. should the Republicans change the Senate rules to prevent Democrats filibustering some of President Bush’s judicial nominees. (Well, OK, not that much interest.)

1.                Washington Post-ABC News Poll April 2005[2]

36. Would you support or oppose changing Senate rules to make it easier for the Republicans to confirm Bush’s judicial nominees?

                                Support                                Oppose                                No Opin.

4/24/05                         26                                          66                                           8

                                             2.[1]           

If these results held for the whole population then some people who would have answered affirmatively to one would have answered negatively to the other, and this, it seems clear to me, would involve them in a contradiction. (Notice, too, that neither of them mentions the word ‘filibuster’ in their question – I wonder why that is?)

1.                    Is the inference justified?

There are three factors that need to be considered.

                                       i.      The sample size: the proportion of the population that is tested.

                                      ii.      The level of confidence: the accuracy level of the extrapolation of the sample’s result to the population. At a 95% level, the result for the population will be within the margin of error 95% of the time. (ie. If you did 100 samplings you would get only 5 whose results would indicate a value for the population that was outside the margin of error.)

                                    iii.      The margin of error: the precision of the result. Generally expressed as ± y %. (eg. Voters are projected to vote Whig at 45% ± 3 %, which means that we have a 95% level of confidence, say, that the result would have been between 42% and 48%).

These three factors are interdependent; changing one affects both the others.

For a result to justify an inference the margin of error has to be narrow enough to make the result non-trivial, and the level of confidence has to be high enough to make the result significant.

Inductive Particularisation

As I said before, inductive generalisations are characterized by the move from facts about particulars to facts about generalities, and as I said in the last lecture, that isn’t the only direction in which an inductive argument can move. There are arguments that go from statistical generalities to facts or claims about particulars. I call arguments of that sort Inductive Particularisations, but you may also see them referred to as Arguments from Statistical Premisses, or Statistical Applications. The argument that I gave as an example, you may recall was this:

                All ravens we have seen have been black

                --------------------------------------------------

The next raven we will see will be black

But this example doesn’t really give you the real flavour of these arguments. That we get from arguments which look like this:

                72% of all Australians are content with their lives

                Robert is an Australian

                ------------------------------------------------------------

                Robert is content with his life

And you may recognise that this is relevantly similar to our old friend:

                Most Australians are happy

                Bob is an Australian

                ----------------------------------

Bob is happy

Note that if you’re going to call these arguments ‘arguments from statistical premisses’ then you’re going to have to accept that ‘most’, ‘some’, ‘a few’, and so on, are statistical quantities. I suppose there’s nothing really wrong with that except that it seems odd. Statistics should have numbers in them, I reckon.

Evaluating Inductive Particularisations

So how should we approach an inductive particularisation?

1.                    Are the premises true?

Once again the first thing to enquire after is whether the premisses are actually true. I’ve noticed in the past that about 70% of all statistics quoted in policy debates are made up on the spot by people who haven’t got a clue what they’re talking about.

2.                    How Strong is the Conclusion?

Obviously the worth of the argument is affected by how strong the conclusion is in comparison with the premiss. If the statistical premiss claims that close to 100% of the population has the claimed property, then it’s going to be much less controversial to conclude that any particular member of that population also has the property. In the case of Robert above, 72% of Australians are happy, but that leaves 28% of Australians not happy, and it wouldn’t be so very surprising if this Robert person was one of that shower of malcontents.

3.                    Is the Reference Class the Appropriate One?

Consider the argument

                98% of people who have their gall bladder removed recover easily

                Martha is going to have her gall bladder removed

                --------------------------------------------------------------------------------

                Martha will recover easily

The statistical premiss we may assume is true. And so is the 2^nd premiss. And the statistical premiss gives a very high probability of recovering – so it might look like the conclusion is a pretty highly likely one, which would make this a very strong argument.

But wait! There’s more:

                98% of 90 year old people who have surgery do not recover easily

                Martha is a 90 year old person about to have surgery

                --------------------------------------------------------------------------------

                Martha will not recover easily

Shouldn’t this be exactly as strong as the previous argument – i.e. very strong? And yet the conclusion is the exact opposite of the previous one. Is there a problem here?

What’s going on here is that the class whose statistical properties are quoted in the statistical premiss and from which the conclusion is drawn – what we call the reference class – is not the appropriate class for the purpose. And what makes it inappropriate is that it fails to meet the requirement of total available relevant evidence. There are facts about the particular (Martha) that make her an exception to the first statistical premiss.

You will find that this suggests a very effective method of criticizing these sorts of arguments. One simply tries to discover whether there’s another reference class which can be plausibly described as the appropriate reference class for the particular in question, for which the inductive particularisation conflicts with the original.

Note on Terms

This is not a course on statistics but I think it’s worth taking a moment to briefly note a related point that is often the source of some confusion. The word average has three quite distinct uses, and we have to make sure we know which of these uses is intended when we try to understand a statement in which it features. It may be the mean, the median, or the mode.

Consider the following five quantities: 180, 40, 25, 15, 15.

i.                   The mean is the arithmetic average. To find it add the numbers together and divide by 5.

Result: 55.

ii.                   The median is the number in the middle of the range (1/2 of the numbers are bigger than it and ½ are smaller).

Result: 25.

iii.                  The mode is the number that is most common.

Result: 15.

Innumeracy

Just as "the average science student" has some essay-phobia, so too "the average arts student" has some maths-phobia. This maths-phobia extends well beyond "the average arts student", pervading many, if not most, corners of society. This phenomenon underlies what we might well describe as numerical illiteracy or innumeracy (following John Allen Paulos) and leads many to hasty acceptance of claims that are based on fallacious mathematical reasoning.

Where arguments include some mathematical reasoning we can reject the argument as invalid if we can show that the mathematical reasoning invoked is invalid. In some cases this ability to critically scrutinize some piece of mathematical reason requires far more mathematical expertise than that possessed by any except the most mathematically proficient. Yet in many cases innumeracy leads us to accept claims based on very simple but nonetheless faulty mathematical reasoning.

The following examples are cases in point.[1]

Example – AIDS Testing

As an example showing how innumeracy can lead one astray consider the following (adapted from one given by Paulos, op. cit., p. 66).

(HYP)     Assume that there is a test for AIDS that is 98% accurate.

                I.e. if x has AIDS then x will test positive 98% of the time and if x doesn't have AIDS

                then x will test negative 98% of the time.

(Note that current testing procedures are much less accurate than this; they test only for the presence of antibodies, the possession of which does not itself mean that one has AIDS.)

Assume also that 0.5% of the population of Australia has the virus — i.e., one person in every two hundred, on average.

Suppose you pop down to the clinic, take a test and receive a positive result. Should you be distraught as a result (i.e. is it rational to be distraught)? In fact the answer is NO!! The explanation is as follows.

Assume 10,000 tests are carried out.

Number of people in (average) sample having AIDS = 0.5% of 10,000 = 50.

Of these, 98% will test positive (by HYP)                                                                       

Number of people having AIDS & testing positive = 98% of 50 = 49.

Number of people in (average) sample not having AIDS = 99.5% of 10,000 = 9,950.

Of these, 2% will test positive (by HYP — since 98% will test negative)                  

Number of people not having AIDS & testing positive = 2% of 9,950 = 199.

In conclusion then:

248 people in every (average) population sample of 10,000 will test positive

yet only 49 of these have the disease.

                Less than 1/5th of all those testing positive have good reason to worry!

The fact that the test is 98% accurate justifies the following conditional claim:

                if you have AIDS then there's a 98% chance of you testing positive.

However the converse conditional (which would justify your being distraught):

                if you test positive then there's a 98% chance that you have AIDS

 is false. What the above basic mathematical reasoning shows is that the following conditional is true:           

                if you test positive then there's less than a 20% chance of you having the disease.

Of course, a positive result will increase the chance of you having AIDS from 1:200 (0.5% ) to 1:5 (20%) so there is reason to be more worried than before the test, yet all is not lost. Far from it.

Some simple mathematical reasoning (not at all the realm of the specialist mathematician) shows that:

to act as if someone has AIDS on the basis of their testing positive will lead to the wrong                 action being taken (at least) 80% of the time.

NB:         Subsequent secondary testing of those with positive results will eliminate most "false positives" (that is, those who tested positive but do not have AIDS) so adequate testing is available. The point is simply that on the above figures a single test returning a positive result provides weak grounds for thinking that the test-subject really is positive.

Even very accurate tests (as with the one assumed here to be 98% accurate) are liable to deliver far more "false positives" than "true positives" (that is, the group of test-subjects                returning a positive test contains far more who do not have what is being tested for than those who do) when the phenomena being tested for is rare (as it is in the above example — only 0.5% of the population were assumed to actually be positive). So, in such situations of testing for rare phenomena, single tests are not a reliable guide to whether someone has whatever is being tested for.[2]

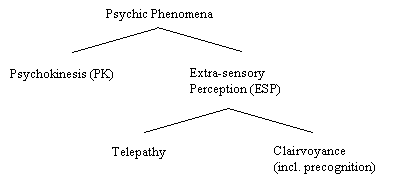
Example – Psychic Phenomena

The phenomena that go under the label "psychic phenomena" or "paranormal phenomena" are typically divided up into what are termed psychokinetic phenomena and phenomena of extrasensory perception (ESP).

§         Psychokinesis is the ability to affect physical events through thought, or an act of will alone, without the mediation of bodily action.       

§         Extrasensory perception (ESP) is exhibited when someone is able to produce information, the acquisition of which cannot be put down to chance or sensory perception.             

o        Clairvoyance is the ability to acquire direct knowledge of events in the non-personal world through means other than the normal sensory channels.          

o        Precognition (a special case of clairvoyance) is where the extrasensory knowledge is of the future.          

o        Telepathy is where the extrasensory knowledge acquired concerns the thoughts or feelings of other persons.

The existence of such phenomena is sometimes supported, it seems to me, by arguments that are deeply flawed, but such arguments sometimes nonetheless succeed because innumerate audiences are prone to accept key "mathematical" assumptions on which the argument depends — such assumptions, they think, are "beyond my ability to assess", thus they simply accept them!

What follows then are two examples of fallacious mathematical reasoning in support of psychic phenomena.

a.                   Predictive Dreams and Precognition

Assume that the probability of having a predictive dream by chance on any given night to be 1/10,000. Then the chances of not having a predictive dream by chance on a given night is:

                1 - 1/10,000 = 9,999/10,000 (i.e. very high).

It follows then that the probability of having two successive nights of non-predictive dreams is:

                9,999/10,000 x 9,999/10,000

and the probability of having only non-predictive dreams all year is:

                (9,999/10,000)­³⁶⁵ = 0.964.

I.e. 96.4% of the population have only non-predictive dreams all year.

Nonetheless, 3.6% of the population do have a predictive dream by chance on some night of the year.

That's a lot of predictive dreams in a year given a population the size of Australia. In fact, if our population is roughly 18 million we should expect about 650,000 instances of predictive dreams due to chance alone during the course of a year!

Hence the following (not uncommon) argument depends for its soundness on bad numerical reasoning:

                (1)           The probability of a predictive dream occurring by chance is so low that the number                                            of actual instances cannot plausibly be put down to coincidence.

So,          (2)           Precognition is a more plausible explanation.

Yet,         (3)           Either predictive dreams happen by chance or precognition occurs.

So,          (4)           The most plausible explanation of predictive dreams is that precognition occurs.

The argument may well be able to be filled out so as to be valid – given some uncontroversial assumptions, were the premises (1) & (3) true the conclusion (4) would be true.

However, it is arguably not sound. Premise (1) would seem to be false; the number of actual instances of predictive dreams is quite plausibly explained by coincidence.

b.                   Telepathy on Demand

                (1)           The probability of cold reading occurring by chance is so low that the number of                                                 actual instances cannot plausibly be put down to coincidence.

So,          (2)           Telepathy is a more plausible explanation.

Yet,         (3)           Either cold reading happens by chance or telepathy occurs

So,          (4)           The most plausible explanation of cold reading is that telepathy occurs.

What are we to say of this argument?

Well, (1) again is questionable if the chance of cold reading occurring has been underestimated.

c.                    General Schematic Argument

                (1)           The probability of an X occurring by chance is so low that the number of instances                                             cannot plausibly be put down to coincidence.

So,          (2)           Y is a more plausible explanation.

Yet,         (3)           Either X happens by chance or Y.

So,          (4)           The most plausible explanation of X is that Y.

Obviously, any argument for Y on the basis of the above argument could be criticized as unsound if (1) is not true - enabling us to reject (2). This could occur in the following way (a possibility obscured by innumeracy):

though the probability of X occurring by chance might be properly estimated as very low, very low probabilities on a very large sample (e.g. human populations) result in a considerable number of actual instances (e.g. low probability of chance predictive dreams in large population yields a large actual number of chance predictive dreams).

Example – Gambler’s Fallacy

The fallacy of thinking that since, say, a fair coin has come up heads eight times in a

row it is more likely to come up tails next throw. (Read Text ch. 10.)