| Logical Arguments | |||
|
|
|||
|
Fundamentals |
|||
|
Argument Strength
In
the last lecture I gave a very general theory of arguments, and you may
recall that according to that account we think an argument is good if it
possess a quality that we called ‘effectiveness’; which is to say
that an argument is good iff it causes the respondent to feel the Argument
Intuition, so that the respondent is more disposed to accept the
conclusion if the other statements are accepted. Now, one consequence of
this very general idea of the goodness of an argument (and it’s a
deliberate consequence) is that it allows us to understand that
arguments may be good to different degrees. If an argument is such that
its effect is that the respondent is only slightly more disposed to
accept the conclusion if the other statements are accepted, then we call
it a weak argument; and if the effect is that the respondent is very
much more disposed to accept the conclusion, then we call it a strong
argument. In
this way we could establish a scale of argument strength. But notice
that on this scale we have fixed points at both ends. At one end we have
arguments that are simply ineffective: the disposition to accept the
conclusion given the acceptability of the premisses is quite unaltered
by the argument. And at the other end we have arguments that are as
effective as they can be: the disposition to accept the conclusion is
overwhelming given the acceptability of the premisses. It is impossible
for us not to accept the conclusion given that we accept the premisses.
It’s this latter class that we’re going to be interested in now. Truth A
fundamental marker that we use for the acceptability of statements is
our attribution of truth to those statements. We think that a true
statement tells us how things really are.[1]
And if we think that a statement is true then we think it’s an
acceptable thing to believe. (It may not be morally uplifting or
beautiful, but it is the right sort of thing to be in our store of
statements about how the world is.) It’s natural, then for us to talk
about a subset of effective arguments in which the acceptability of the
statements is interpreted in terms of the truth of the statements. In
that case the scale of argument strengths could be interpreted as
referring to the likelihood (or the perceived
likelihood if you prefer) that the conclusion is true given that the
premisses are true. We could thus arbitrarily distinguish 5 levels of
strength to get a scale that looks like this: 1.
A useless argument is one in which the truth of the premisses has
no effect at all on the truth of the conclusion. 2.
A weak argument is one in which the likelihood of the
conclusion’s being true is not much affected by the truth or falsity
of the premisses. 3.
A moderate argument is one in which the likelihood of the
conclusion being false if the premisses are true is quite low. 4.
A strong argument is one in which the likelihood of the
conclusion being false if the premisses are true is very low. 5.
A valid argument is one in which it is just impossible for the
conclusion to be false if the premisses are true. It’s
this very last level that we’re interested in. In fact, I’ll
separate it from the rest because the term that I used there is a
technical term in philosophy that shouldn’t be mixed up with the
vernacular terms that I used to name the other levels. Validity D1.
An argument is Valid if and only if it is impossible for the premisses to be true
and the conclusion false And
there’s also the obvious counterpart notion of invalidity. D2.
An argument is Invalid if and only if it is possible for the premisses to be true
and the conclusion false What sorts of arguments are valid? Well, I’ve been using one for an example pretty regularly. It’s the old Socrates example: All men are mortal
Socrates is a man Socrates is mortal It seems clear to everyone that it is impossible for the premisses to be true and the conclusion false. And, of course, it’s not difficult to find examples of invalid arguments either. For example: All men are mortal
Socrates is mortal Socrates is a man Here we can very well imagine that the premisses could be true but the conclusion false. Socrates might be the name that I give to a pet fish for example. It’s pretty obvious why we think that validity is valuable. It’s because when we can recognise that an argument is valid we can be assured that the argument won’t take us from true beliefs to false beliefs. Using valid arguments is epistemologically safe; or rather, using valid arguments properly is safe, because validity isn’t the only thing that’s important when we want to use arguments or to evaluate them. To see this, notice two things: 1. Valid arguments can have false premises. (It's just that if they were true then the conclusion would be too). For example: Socrates
is a wombat All
wombats are Greek Socrates
is Greek To ensure that an argument has a logically compelling
conclusion we need to also ensure that we start from true
premises, as well as ensuring that true premises force a true
conclusion (i.e. validity). 2. Valid arguments can have false conclusions. Socrates is a wombat All wombats are Spanish Socrates
is Spanish Valid arguments simply rule out moving from true
premises to a false conclusion. They do not tell us whether the premises
or conclusion actually are true. Soundness What
we’ve just said means that to unequivocally establish a conclusion as
true by means of argument we require that:
We
need a name for these sorts of argument. The technical term for them is
Sound. So: D3. An argument is Sound
if and only if it is valid and has true premisses. Such
an argument must have a true conclusion. By
validity:
were the premises true the conclusion would have to be true And:
the premises are true. So:
the conclusion must be true. If confronted by an argument whose conclusion you think is false, you are thereby committed to either the falsity of some premise, or the invalidity of the argument. Puzzle for Fun:Which
if any of the following arguments is valid? John is both in the room and not in the room
John is Bulgarian
John is Bulgarian
John is either in the room or he is not Form Some
valid arguments are valid because of the form
of the statements that occur in them. For example, the argument
that: All men are mortal Socrates is a man Socrates is mortal is
valid: and any argument that has the form
All A are B
X is an A
X is a B is
going to be valid whenever the A, B, and X are uniformly replaced by
some appropriate phrases or names. The sort of form that allows us to
tell whether another argument of the same form is going to be valid is
called the Logical
Form of the argument Arguments
of that sort seem to be quite different from a valid argument such as:
Socrates is a bachelor Socrates is unmarried. There
doesn’t seem to be any information about the validity of the argument
in its form. We distinguish
the first kind of argument as being Formally Valid. They are a very important type of argument
because – if they are done right – they can be shown to be as strong
as any argument can be. It is arguments of this sort that form the
subject matter of Logic. We can think of them as the logical arguments. There
are two main classes of logical arguments that we will consider here.
They go by the name of Syllogistic and Propositional logic.
[1]
Actually many books have been written about what truth actually is.
What I’ve just said is just one theory, but it’s the one that
most people think is most reasonable.
|
|||
|
Propositional Logic |
|||
|
Propositional Connectives As
the name suggests, propositional logic (also once known as sentential
logic) is concerned with the relations between propositions themselves,
or between the sentences which represent them. This is a type of
argument first considered systematically by the Stoics – especially
Chrysippus – but all their work was lost and the modern study did not
begin until the 19th C. with George Boole. We
know that some sentences are true and that sentences can be built up
from other sentences in many ways, but we find that there are some ways
of joining sentences together to make new sentences that are special
because the truth of the resulting sentence is a function only of the
truth of the smaller sentences that go to build it. The function that is
applied is indicated by the words that are used to stick sentences
together. The
standard words that we consider are: 1.
‘or’ for disjunction
‘Grass
is green or snow is white’ is true if ‘grass is green’ is true or
‘snow is white is true’ Of
course, this being English, we can’t just blindly look for just that
sort of obvious structure in a sentence as a marker for a disjunction.
For example we also have a disjunction in a sentence like: Grass
or leaves or mulch make a good compost. And
in cases like this we recognise that there is a disjunction because we
can reconstruct it – without changing the meaning – as: Grass
makes a good compost or leaves make a good compost or mulch makes a good
compost. And
there’s also the problem of knowing just what is meant by the
‘or’, because there are at least two kinds. 1. exclusive (xor) We’ll have hamburgers or pizza for dinner
(but not both.)
2.
inclusive
There’s a pen or a pencil in that drawer (or both.)
2.
‘and’ (‘but’, ‘as well as’, …) for conjunction ‘Grass
is green and snow is white’ is true if ‘grass is green’ is true
and ‘snow is white is true’ ‘Grass
and trees are plants’ 3.
‘not’ (‘it is not
the case that’, ‘no’, …) for negation ‘Grass
is not green’ is true if ‘grass is green’ is not true. ‘It
isn’t the case that grass is green’ 4.
‘if … then ---’ for implication ‘If
grass is green then snow is white’ is true if in any case that
‘grass is green’ is true it is also the case that ‘snow is white
is true’. Given
sentences that use such truth operators or their equivalents we can
construct arguments. Here’s a couple of very important forms of
arguments that we can get using just these resources. Disjunctive Syllogism: P or Q Not Q
P You are English or you are French. You are not French. So, you are English. Hypothetical Syllogism: If P then Q If Q then R If P then R If you are English then you like fish and chips. If you like fish and chips then you are fat. So, if you are English then you are fat. Truth Tables There
are effective methods for discovering whether such arguments are valid.
The easiest method is by making a table of truth values. We
want to know whether it is possible for the premisses to be true and the
conclusion to be false so we make up a table that will allow us to see
whether there is some assignment of truth values to the parts of the
premises that will make those premises true and the conclusion false. To
do so we use the following definitions for the truth functions. 1.
A
B
A or B
T
T
T
T
F
T
F
T
T
F
F
F 2.
A
B
A and B
T
T
T
T
F
F
F
T
F
F
F
F 3.
A
not A
T
F
F
T 4.
A
B
if A then B
T
T
T
T
F
F
F
T
T
F
F
T We
combine these functions in the truth tables.
For the disjunctive syllogism A
= You are English
B = You are French
A
B
A or B
not B
T
T
T
F
T
T
T
F T
F
T
T T
F
F
T
For the hypothetical syllogism D
= You are English
E = You like fish and chips
F = You are fat
D
E &n˙˙˙˙
F
if D then E
if E then F
if D then F
T
T
T
T
T
T
T
T
F
T
F
F T
F
T
F
T
T T
F
F
F
T
F F
T
T
T
T
T
F
T
F
T
F
T F
F
T
T
T
T F
F
F
T
T
T
|
|||
|
Conditionals |
|||
|
Conditional Statements Before
we move on to talk about the other important division of logic, we
should talk a little bit about those statements that are constructed
from other statements using the ‘if … then ---’ connective,
because they turn out to be very important in arguments. The
first thing to note is that there is a vocabulary associated with them. D4. a.
A statement of the form ‘if P then Q’ is a Conditional
Statement. b.
In a statement of the form ‘if P then Q’ the constituent statement P
is the Antecedent c.
In a statement of the form ‘if P then Q’ the constituent statement Q
is the Consequent Of
course, language being the flexible thing that it is, not every
conditional statement has to have just that form. The following are all
equivalent
If P then Q
P only if Q
If P, Q
Q if P
Unless Q, not P From
a more general point of view a conditional statement coordinates two
parts, the antecedent and the consequent. It claims that any situation
in which the antecedent (P in the case above) is true is also a
situation in which the consequent (Q here) is true. (Note that it says
nothing about situations in which the antecedent is not true.) Generally,
the first thing you should do when you see some sort of conditional
statement is to put it into standard form so that you will not be misled
by an unfamiliar or perverse phrasing. Note that in the last two forms,
for example, the consequent occurs before the antecedent, which
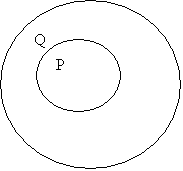
may lead to confusion. A diagram may help to understand what a conditional is saying. The conditional ‘if P then Q’ can be drawn as: |
|||
|
|
|||
|
(Think
of the circle labelled P or Q as representing the collection of all the
situations in which P or Q is true.) Necessity and
Sufficiency Another
way to look at it is to say that the conditional statement claims: that
a situation in which P is true is a sufficient
condition for Q to be true, and that a situation in which Q is
true is a necessary condition for P
to be true. When
P is a sufficient condition for Q and also a necessary condition for Q,
then we say it is a necessary and sufficient condition for Q. Note
that if P is a necessary and sufficient condition for Q then Q is also a
sufficient and necessary condition for P. (To get a feel for this try
drawing the pictures.) In such a case it would be true that:
If P then Q and if Q then P. This
is a biconditional.
We write this more succinctly, by combining some of the non-standard
forms above, as: P if and only if Q Arguments Note
that a very common mistake for people who are just beginning to study
this sort of thing is to think that conditional statements are
themselves arguments. They are not; but as I mentioned before they do
play a role in a great many types of argument. We’ve already seen the
hypothetical syllogism, now here are two more types of argument that are
very important: Modus ponens: If P then Q P
Q If you are English then you like fish and chips. You are English. So, you like fish and chips. Modus tollens:
If P then Q Not Q
Not P If you are English then you like fish and chips. You do not like fish and chips. So, you are not English. There
are also two very common errors in arguments related to these formally
valid arguments. They are formal fallacies because they result
from an error in the very form of the argument. Affirming the consequent: If P then Q Q
P If you are English then you like fish and chips. You like fish and chips. So, you are English. Denying the antecedent: If P then Q Not P
Not Q If you are English then you like fish and chips. You are not English. So, you do not like fish and chips. Of
course you can use the method of truth tables to satisfy yourself that
these arguments really have the qualities that I’ve just claimed. You
don’t have to take any of this on faith.
|
|||
|
Syllogistic Logic |
|||
|
The
other type of logic that I mentioned treats a type of argument that was
first considered by Aristotle, the founder of Western logic. Unlike
propositional logic, the fundamental parts of syllogistic logic are the
terms that name classes or categories, and the logic deals with
relations between classes or categories – thus it is sometimes called categorical
syllogism (syllogism just means deduction in Greek). The
Socrates example that I began with is the classic example of a syllogism
(even though it isn’t one!) Categorical
Propositions The
relations between categories that can be treated purely formally are
those of inclusion or part inclusion. Other relations have been tried
but they turn out to be hard or useless. The categorical propositions
that express these relations are of four possible forms: 1.
All S are P
Universal Affirmative
A 2.
No S are P
Universal Negative
E 3.
Some S are P
Particular Affirmative
I 4.
Some S are not P
Particular Negative
O where
S and P are names of categories (standing for Subject and Predicate.) We
can make some arguments using quantifiers such as many, few, most, at
least two, etc., but we can’t make very useful arguments with them –
at least not with the formal
techniques we’re looking at here. Syllogistic
Arguments Given
two categorical propositions as premisses we can sometimes draw a
conclusion in the form of another categorical proposition. Ex 1. No G are H
All F are G
No F are H
No men are perfect
All Greeks are men
No Greeks are perfect Ex 2. No G are H
Some F are G
Some F are not H
No philosophers are wicked
Some Greeks are philosophers
Some Greeks are not wicked There
are rules for finding the possible conclusions for such set of premisses
but we won’t go into those here. Do note however that there can be no
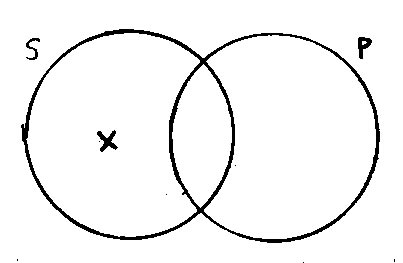
more than three categorical terms involved. Venn Diagrams We
can assist our intuitions about categorical arguments by the use of Venn
diagrams. In a Venn diagram for a categorical statement with two
terms in it we draw two overlapping circles, then we put a cross in a
position to represent some object that the statement claims to exist, or
we shade all those parts of the diagram where the statement says that no
object can be. It’s easier to see this with pictures. [Draw diagrams on board] 1.
All S are P
2.
No S are P
3.
Some S are P 4.
Some S are not P
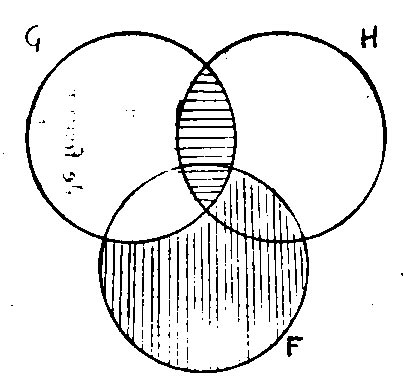
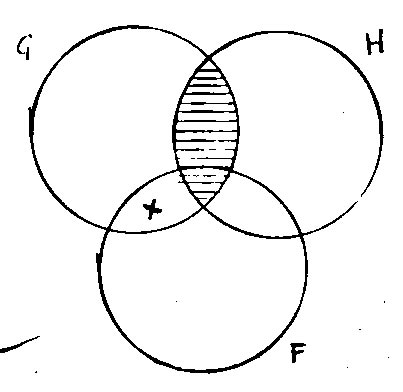
To
test whether a syllogistic argument is valid, draw a diagram for the
first premise; then over the same diagram indicate the conditions for
the second premise using a third circle to represent the term not
already present in the first premise. If the resulting diagram is
consistent with the situation of the conclusion then the argument is
valid. That
sounds complicated but some worked examples make it clear what is going
on. [Draw diagrams for:] Ex 1.
Ex 2.
|
|||
|
Showing Validity |
|||
|
Showing
that an argument is formally valid — i.e. showing that it has the
right logical structure — can be done either formally or informally.
Formal means for showing validity (and invalidity, for that matter) are
the domain of Formal Logic and are too detailed for us to pursue here.
(The PHIL1020 course is devoted to this.) Instead we shall simply
suppose that: (i) there are some simple, uncontroversial cases of valid reasoning. (E.g. modus ponens,
modus tollens, disjunctive syllogism and hypothetical syllogism.) And
then: (ii) given any argument for consideration, we will consider it to be valid just in case we can
show that its conclusion can be inferred from the premises by use
of these simple steps
or rules. Showing
validity in this way then is a matter of showing that the argument in
question has the right kind of logical structure by showing that its
conclusion can be derived from the premises in accord with the basic
steps or rules of good reasoning. An Example Step
1
What is the argument to be analysed? Ned
Kelly was either an outlaw or a political activist. If he was an outlaw
or a killer, he deserved what he got. Only if he was fairly tried and
justly hung did he deserve what he got. But he was not fairly tried.
Therefore, he was a political activist. Step
2
How are we to evaluate the argument?
By attending to its structure or logical form. Using
the following abbreviations: O
- Ned Kelly was an outlaw; P
- Ned Kelly was a political activist; K
- Ned Kelly was a killer; D
- Ned Kelly deserved what he got; T
- Ned Kelly was fairly tried; H
- Ned Kelly was justly hung. the
argument can be formalized as follows: O or R
if (O
or
K) then
D
if D then (T
and
H)
not
T
R Step
3
Is the argument above valid or invalid?
Valid. I can prove it as follows:
Step
4:
By assumption, if (O
or
K) then
D, and
if D then (T
and
H), so (1)
if (O or
K) then
(T and H)
[since the basic rule: 'If A then B, If B then C; hence If A then
C' is valid].
But, by assumption, not-T, so (2)
not-(T and
H)
[since the basic rule: 'not-A; hence not both (A and B)' is
valid]. (3)
So, by (1) and (2), not-(O
or
K)
[since the basic rule of modus tollens is valid]. (4)
So, neither O
nor
K
[since the basic rule: 'not-(A or B); hence neither A nor B' is
valid]. (5)
So, by (4), not-O
[since the basic rule: 'neither A nor B; hence not-A' is valid].
Yet, by assumption, O
or
R. (6)
Hence, by (5),
R
[since the basic rule: 'not-O, O or P; hence P' is valid]. Such proofs are often not an easy matter and can sometimes take great ingenuity, imagination and insight. We shall focus on showing invalidity — generally an easier task.
|
|||
|
Showing Invalidity |
|||
|
It
is one thing to think that an
argument is invalid, another for it to actually be invalid, and yet another to be able to show this. We shall look at two methods for establishing the
invalidity of an argument. Method 1: Counterexamples To
show an argument X is invalid we can simply point to arguments having
the same structure as X which are clearly invalid — i.e. find an
argument with the same structure which has obviously true premises and
an obviously false conclusion. This will show that argument X has an
invalid form and so is invalid. In
other words, to show that argument X is invalid — that the conclusion
does not follow from the premises — we need only show that argument X is
just like arguing according to some argument Y, where Y is clearly
invalid.
So,
applying this, consider the argument (2):
If God created the universe then the theory of evolution is wrong
The theory of evolution is wrong
God created the universe If
this is valid then it must be because it has a valid logical structure
or form. So, any argument of this form will be valid. But arguing
according to (2) is just like arguing:
If Dominic is a wombat then Dominic is a mammal
Dominic is a mammal
Dominic is a wombat This
latter argument has the same structure and is obviously invalid. Premises are obviously
true and conclusion is obviously
false! So it follows that (2) does not have valid logical structure and
so is invalid. Applying
to argument (4).
If God created the universe then the theory of evolution is wrong
God did not create the universe
The theory of evolution is not wrong
That's
just like arguing:
If Dominic is a wombat then Dominic is a mammal
Dominic is not a wombat
Dominic is not a mammal which
is clearly invalid. So, (4) must be invalid. Method 2: Invalidating Possible Situations Another
method for showing that an argument is invalid establishes directly that
it is not impossible for the
premises to true and the conclusion false by showing how it is possible
for the premises to be true and the conclusion false. Consider
some argument:
A
It can be shown to be
'A' can be true
B
® invalid
if we can show that
® 'B' can
be true
C
'C' can be false
in the same situation.
The claim that an argument is valid amounts to the claim that any situation which makes the premises true makes the conclusion true, so, pointing to a possible or conceivable situation that makes the premises obviously true yet the conclusion obviously false will clearly show that the argument is invalid.
E.g.
Fallacy of affirming the
consequent
If my car is out of fuel, it won't start
My car won't start
My car is out of fuel. Consider
now the following possible situation. My car will indeed not start without fuel (it is a fuel-driven car) and the
electrical
won't start). Yet The
premises are obviously true in this situation and the conclusion is
obviously false. The
situation is not impossible (i.e. it is possible).
So,
it is not impossible for the premises to be true and the conclusion
false. So,
the argument is invalid. E.g.
Fallacy of denying the
antecedent
If the Committee addresses wilderness value then it must address
naturalness.
It will not address wilderness value.
It need not address naturalness.
Consider now the following possible situation. Wilderness value involves, amongst other things,
naturalness (Federal legislation actually defines 'wilderness value'
this way). Moreover, the Committee's terms ofreference do not include
consideration of wilderness value (so it won't address it). Yet the Committee is explicitly
formed to consider naturalness (to feed their findings into those of
other Committees, so that a joint finding can be made regarding
wilderness values).
The premises are obviously true
in this situation and conclusion obviously
false.
The situation is not impossible (i.e. it is possible).
So, it is not impossible for the premises to be true and the
conclusion false. So, the argument is invalid.
|
|||